Threshold cryptography exists in obscurity relative to more widely exposed concepts in security: encryption, digital signatures and certificates, for example. Although academic cryptography experts tend to have good familiarity with Shamir’s Secret Sharing Scheme and Blakley’s Scheme, a great many industry practitioners are unaware of these algorithms and how their implementation can offer tremendous benefits within an existing cybersecurity tech stack. 

In this post we explore three topics:

1. Reasons why threshold cryptography isn’t well-known,
2. How threshold cryptography works, and
3. Reasons why it makes sense to connect threshold cryptography with encryption keys.

First, the two main reasons why threshold cryptography isn’t well-known.

Threshold cryptography seems useful only in niche circumstances.

Threshold cryptography – often referred to as “secret sharing” is a mechanism for sharing information among a group of participants. It is easily understood by example: Alice, Bob and Charlie are siblings. Their father, David, has diamonds in a safe deposit box, which can be opened with a passcode. David loves his children but doesn’t entirely trust them. He wants to make sure the safe deposit box is accessible upon his demise, but only upon the agreement of at least two of his children.  To achieve his goal, David can employ Shamir’s Secret Sharing Scheme (SSSS) to provide each of his children with a portion of the passcode, but not enough to act alone.

We will get into the mechanics of how SSSS works momentarily but let’s pause here to make an important observation: secret sharing isn’t broadly useful in an information security context in the same manner as encryption. With respect to encryption, it is intuitive that we don’t want anyone snooping on the password sent from users to their bank’s websites for online transactions. Similarly, the utility of physical signatures is obvious even at a young age, and digital signatures are easily understood as the 1s and 0s equivalent of signing one’s name with a pen. It isn’t remotely as clear as to the utility of threshold cryptography under ordinary circumstances (i.e., when one isn’t trying to split the passcode to a safe).

Threshold Cryptography is hard to implement with a reasonable user experience.

Let’s get back to David’s quandary regarding his safe deposit box. Let’s assume he chooses to go forward with his plan to use SSSS to split the code among his children. There are some command line tools that allow David to split a secret. There are even websites that let David take SSSS for a test drive. But once David has split the secret into components, then what?  Is he to distribute on paper the pieces of the secret to each of his children and have them each hide their notes in their respective sock drawers?  It just doesn’t seem all that practical.  It might make sense to engage in this sort of charade for high-value information, such as bitcoin keys (and, indeed, there is software to do so), but it certainly isn’t as simple as the average app on a smartphone.

So, there you have it.  The utility of threshold cryptography isn’t obvious and it isn’t easy to implement with a reasonable user experience. That is why AES-256 is so widely known while threshold cryptography languishes in obscurity.  

So is that all to the story? 

Before we throw in the towel and conclude that SSSS isn’t particularly useful, let’s take a look at how SSSS actually works.  It is surprisingly easy to understand.

Threshold cryptography: under the hood.

Shamir’s Secret Sharing Scheme and your nightmares about high school geometry.

A few concepts from high school geometry:

1. On a cartesian plane, you need two points to define a line. With just those two points, you know everything there is to know about the line.
2. One point isn’t sufficient to define a line – an infinite number of lines could pass through that one point.
3. Using two points to define a line, we can calculate any number of additional points on that line, and use any set of two of the additional points to define that very same line.

Concept 1:  On a cartesian plane, you need two points to define a line. With just those two points, you know everything there is to know about the line.  For example, we know the Y intercept with certainty.

In understanding SSSS, let’s say the Y intercept is our secret. Alice and Bob each know one of the points on the line. Together, they can draw the line exactly as it should be, and they know the Y intercept – David’s passcode. 

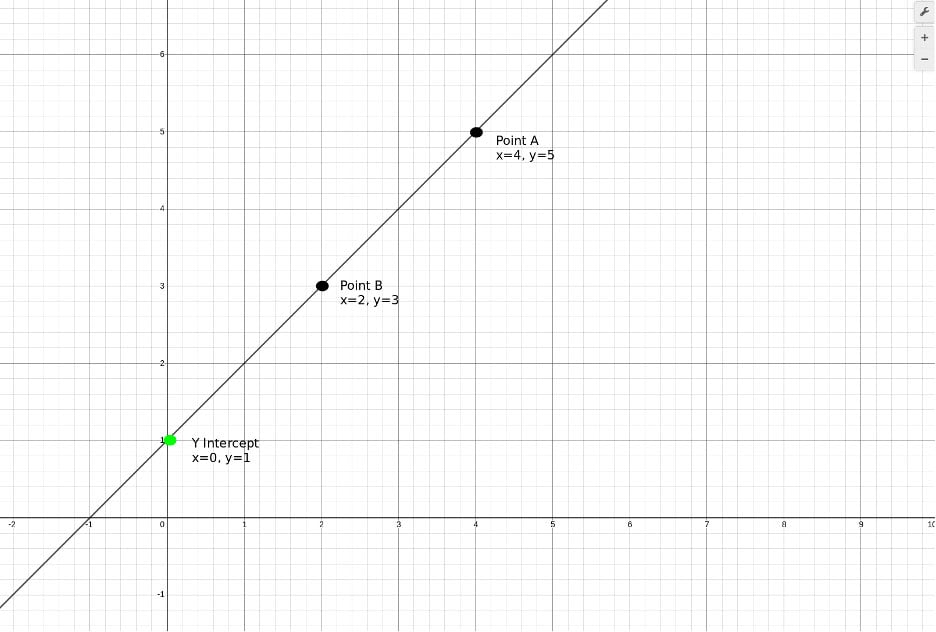
Figure 1: Only two points are needed to define a line and know its Y-Intercept with certainty.

Concept 2: One point isn’t sufficient to define a line - an infinite number of lines could pass through that one point.  In other words, Alice, acting on her own, doesn’t have sufficient information to draw the line and therefore cannot know the Y-intercept.

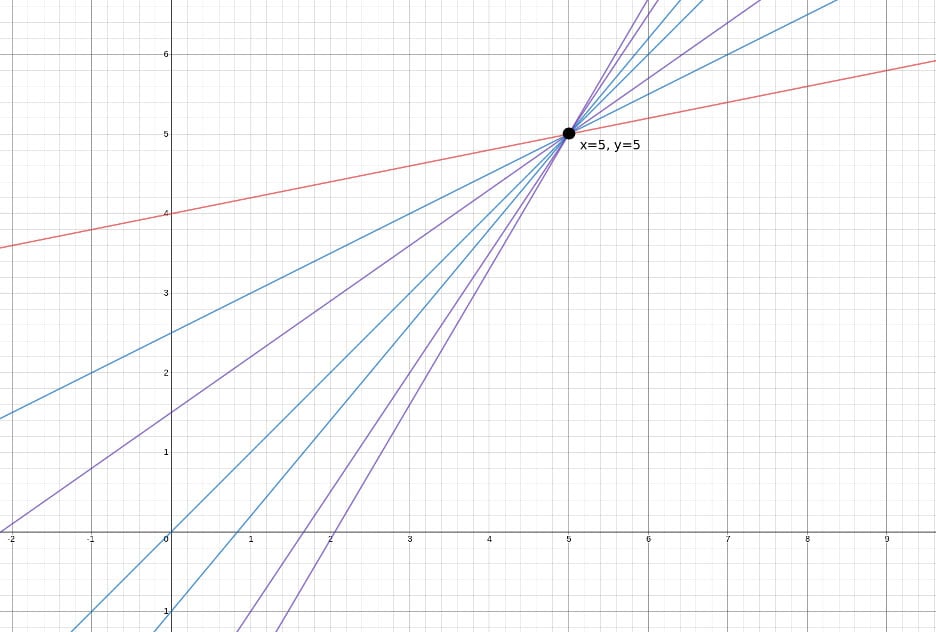
Figure 2: An infinite number of lines pass through point (5,5).

Concept 3:  Using two points to define a line, we can calculate any number of additional points on that line, and use any set of two points to define that very same line.  We can add Charlie into the mix simply by providing him another point on the line.  Now, Charlie can coordinate with either Alice or Bob to draw the line and determine the Y-intercept.

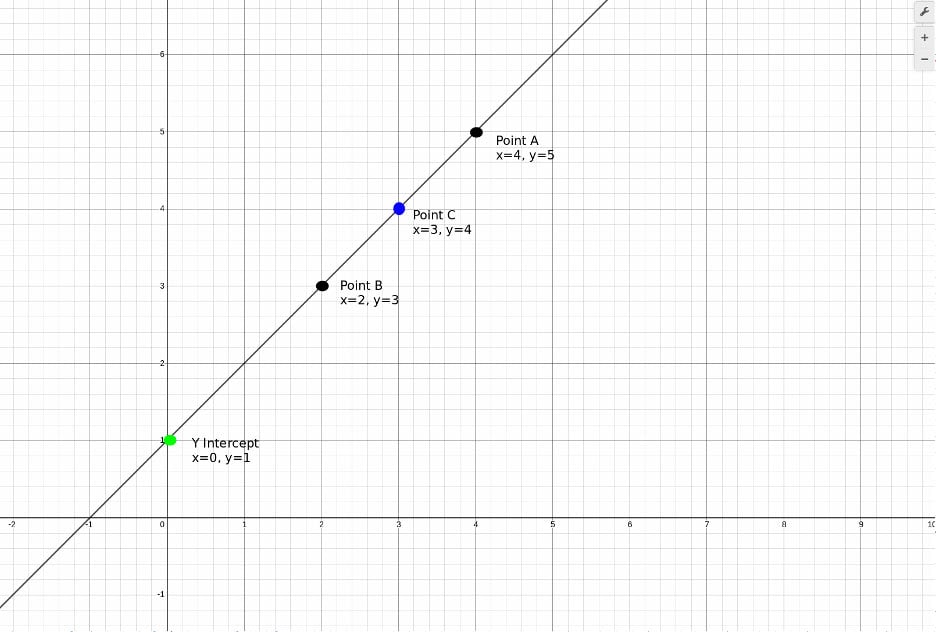
Figure 3: We can add a third point to the line, point C, and then use either A and B to define the line, or A and C or B and C.

So, there you have it! SSSS in a nut-shell. With simple geometry, we can share a secret among a group of participants, providing none of the individual participants with sufficient information to  access the secret but enabling a subset to coordinate to determine the secret. 

(To be fair, we’ve over simplified our explanation a little bit. In a real implementation of SSSS, the math would all be done in a finite field, but the above provides the framework).

Some pretty cool features of SSSS.

These deserve a mention:

1. We can add as many participants as we want simply by articulating more points on the line. If Alice, Bob and Charlie have five more siblings, that is no problem.
2. Our example of SSSS provides nice redundancy: we could have a dozen participants and even if ten disappear, we’re still in fine shape.
3. Just as two points define a line, three points define a parabola (an equation in X²). We can require that three participants coordinate to reassemble a secret by using a parabola instead of a line. And we can go further: four points define an equation in X³, five points for X⁴, and so on and so forth.

Configurations in threshold cryptography are often referred to as M-of-N configurations.  By that, we mean that a total of N people (or devices, pieces of paper, etc.) have pieces, or shards, of the secret and that any M participants can collaborate in order to reveal the secret.

Understanding how SSSS works also further accentuates how awkward it can be to utilize. Each of the participants needs to store securely his or her piece of the puzzle and then when it comes time to reassemble the secret, a sufficient number of participants must come together to do so.

Now that we have reviewed how threshold cryptography works, let’s talk about encryption.

Using threshold cryptography for encryption keys

Symmetric ciphers, such as AES (and Triple DES) have been around for decades. They’re used frequently in a variety of applications. In fact, AES is so important and popular that most modern CPUs have instructions built-in for hardware implementations for it. As you read this blog post right now, your connection to the server uses HTTPS which, in turn, (generally) uses AES for the underlying encryption of traffic. In a certain sense, AES is ubiquitous.

Of course, a key is needed every time AES is used. The generation and storage of that key ranges in difficulty from relatively trivial to being a royal pain-in-the-neck, depending on the circumstances.

Encrypting data in transit during an HTTPS session falls into the relatively trivial camp. A Diffie-Hellman Key Exchange (or perhaps an Elliptic Curve DHKE) occurs on the fly, at the initiation of the session. That key, or a derivative of that key, can be used for AES. The key is ephemeral in nature: it needn’t be stored after the session is over. With respect to key storage, encrypting data in transit presents fewer challenges than encrypting data at rest.

Encrypting data at rest is a different story. Keys are not ephemeral but rather they must be stored securely for future use. In general, the storage mechanism involves some sort of password based system: (a) hashing a password, (b) encrypting keys with asymmetric ciphers which, in turn, involve passwords or (c) storing keys on a central server accessible via… you guessed it… a password. This creates problems: 

• Users hate passwords,
• Passwords for encryption keys cannot be regenerated if lost, and
• Centralization of keys creates a honeypot for attackers.

Basically, we’d all be a lot better off if we could store encryption keys without the involvement of passwords, which brings us back to the idea of using threshold cryptography. The example of David and his three children provides a good backdrop for how we can split encryption keys into pieces. But there is a problem we must overcome: just as we pointed out earlier in this article, it would be rather inconvenient to store the pieces of the keys on paper and rely on the participation of several people in order to decrypt our files. 

Fortunately, there is a much better way. We can take the keys, split them into pieces and store them on our own computers, smartphones, tablets, etc. That is precisely what we do at Atakama. The encryption process is as follows: 

1. Create a file,
2. Generate a new key on the host machine on which the file was created and encrypt the file with that key, using AES,
3. Split the key into pieces, and
4. Keep one piece on the host machine, send another to the user’s smartphone, another to a user’s tablet, etc.

Then, when it comes time for the user to access the file:

1. Have the filesystem request the relevant pieces of the key,
2. Reassemble the key,
3. Decrypt the file, and
4. Have the file open in whatever program it normally would.

And here we have it - by marrying threshold cryptography with encryption, we enable the encryption of data at rest without the use of passwords.  Furthermore, because we can create as many pieces of the key as we wish, we can have as much redundancy as we would like regarding the safety of key storage.

Atakama’s core innovation is the creation of a fully distributed system combining traditional encryption with threshold cryptography, all with an easy-to-understand user interface.

Atakama works by encrypting each object (file) with its own unique key, splitting the key into pieces, and then distributing the pieces of the key among several devices. Consequently, an attacker would need to hack into multiple, physically separate devices in order to access a user’s data.

By encrypting each file individually, we render a breach almost completely useless to the attacker. The most an attacker can access is a file in use at the exact time of the attack, which is a vast improvement over the status quo.